1. Project Background

Economic dispatch problem can be solved by simplifying the original problem with objective functions of reducing the total generation cost with constraints. The conventional methods are lambda-iteration approach and Lagrange multipliers function. These two methods could be applied when the fuel cost function of the generation set is convex. More researchers provide new techniques for economic dispatch problem (EDP). However, most of these methods have to be operated by a control center that can access the state of the whole system. In the future, with the anticipating smart grid will have a large amount of geographically distributed energy resources (DERs), the conventional centralized control system may not be able to handle the massive amount of data flow effectively.

Due to the number of controllable devices (e.g., DERs) has been increased rapidly in the grid, distributed algorithms have been introduced on power system applications. The similarity between the EDP and distributed algorithm such as formation control is that both the basic elements (incremental costs of generators and the velocities of Unmanned Aerial Vehicles) reach the consensus. Thus, extensive studies have been performed on applying consensus algorithm to solve power system problems.

Extensive studies have been done by scholars in the power systems research community. One of such applications is solving EDP by consensus algorithm. Estimation of power mismatch is introduced to improve the incremental cost consensus (ICC) method in. Implementing the algorithm into a real ARM based microcontroller is proofed to be feasible. An auction based algorithm with transmission line considering extend the application prospect of the algorithm has been introduced in . Besides those studies, factors utilized to optimize ICC for EDP such as sampling rate and wireless communication are also been discussed. Despite the great progress on theory development, the performance of distributed control algorithms on more realistic power system models has not been thoroughly studied.

Simulation model used in this study is demonstrated in Figure 1. The IEEE Fourteen bus system has been used as the physical layer of our simulator; a distributed controller is embedded for each generator in the power system in order to build the communication and control layer for LICC algorithm.

Conventional distributed optimization treats the current power demand as the initial condition of the system; then it applies optimization algorithms to solve EDP. When the power demand increases, the optimization has to be reinitialized for the new condition. The leader follower Incremental Cost Consensus (ICC) algorithm was proposed to solve the classical EDP in a distributed fashion. In that leader follower ICC given by, the leader uses the total power demand as the input reference signal to lead the group move towards the optimal operating condition. This paper processed a LICC algorithm that can solve the problem without a leader by maintaining a distributed estimation of the total power mismatch on local agents.

With the LICC algorithm, the grid optimal operating condition can be reached based on local information exchanges. A detailed generator model with excitation system and prime mover have been built in order to simulate the dynamics of generators in a more realistic scenario. Simulation results demonstrate the effectiveness of LICC algorithm on a detailed power system model. In this paper, we have shown that the steady state solution of the LICC controlled system is equal to the optimal solution of EDP. Simulation results from the detail simulator have demonstrated the global optimality can be reached with properly designed system configuration and parameters.

Figure 1. General model display

2. LICC algorithm and detailed models

       2.1 LICC algorithm for EDP

           

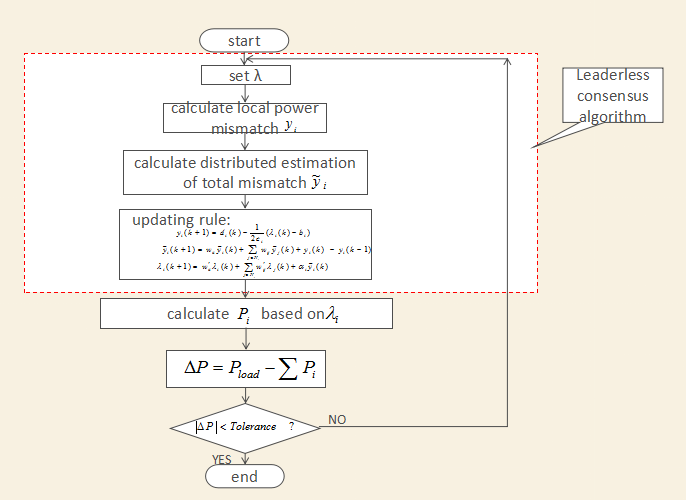
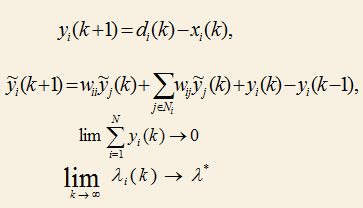
Figure 2. LICC flow chat

From the praph on above, we can see the general steps for solving EDP by LICC algorithm

,where W denotes the weighting matrix for the consensus updating way, the xi means the power generated in the i-thbus, the di represents the power demanded in i-th bus. Lamda is the incremental cost of the generator.

It is a distributed algorithm because each agent only needs the information for its one hop neighbors and itself, there is no multi hop routing algorithm required. The distributed algorithm can be viewed as a discrete time linear system. Note that the generation limits will be handled automatically because only real local mismatch information has been used as the feedback. If a generator reaches its limit, the output power will not change, which will be reflected on the local mismatch.

     2.2 implemente the method into real time simulator

In order to validate the proposed LICC on a realistic scenario, we consider an IEEE Fourteen bus test system as our simulation testbed. In the testbed, five generators serve the total load. We define the fuel cost function for each generator and the objective is to solve EDP as well as guarantee the power quality.

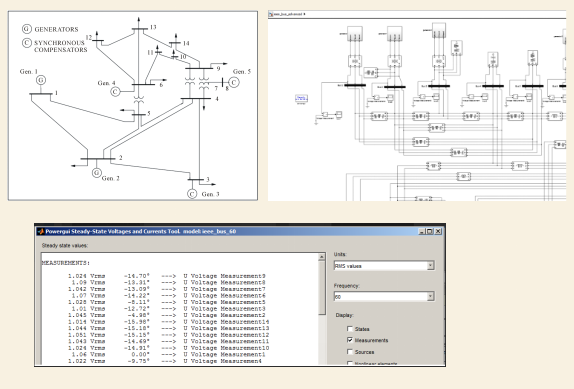
Figure 3. IEEE 14 bus model for steady state

We build a Matlab Model in Simulink, and according to the parameters of addmitance matrix of IEEE 14 bus system, we set the parameter. With the results from the Powergui, we could study the steady state of the power system model. Also, power flow has been solved in Powemat by UIUC power group. I use that solution as the reference to campare the difference with the simulation result.

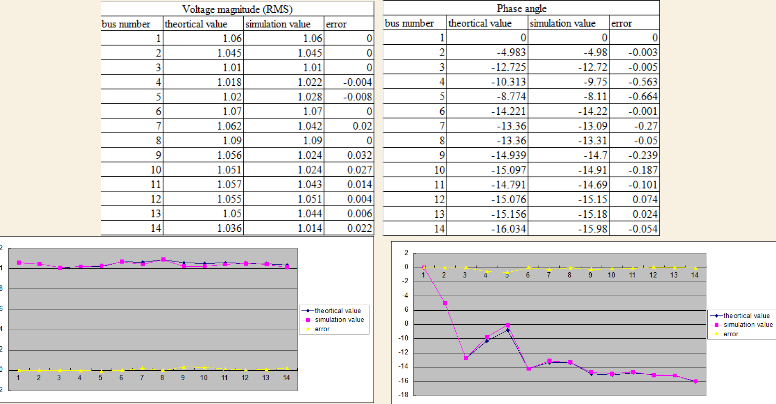
Figure 4. correction proof for bus model

The conclusion is that our simulation model could be reflect the feature of the IEEE 14 bus model.

The generation system is created by the following process:

In order to make generators perform economic dispatch and maintain power quality. AGC is implemented for frequency regulation. For the same reason, AVR is also contained in the generator system. The frequency and the voltage have been controlled separately, the frequency is managed by prime mover system and the voltage is regulated by the excitation system.

The parameter of generators in this paper is given as: The nominal output power Pn =200 MW, the nominal phase to phase voltage Vn =15kV, frequency fn =60Hz, number of poles =20, inertia constant of the generator H =2.9.

The IEEE 14 bus test system is chosen as the testbed for the LICC algorithm. Three phase Pi section line model represents the transmission line in the power system; generation system is utilized to denote the power resource.

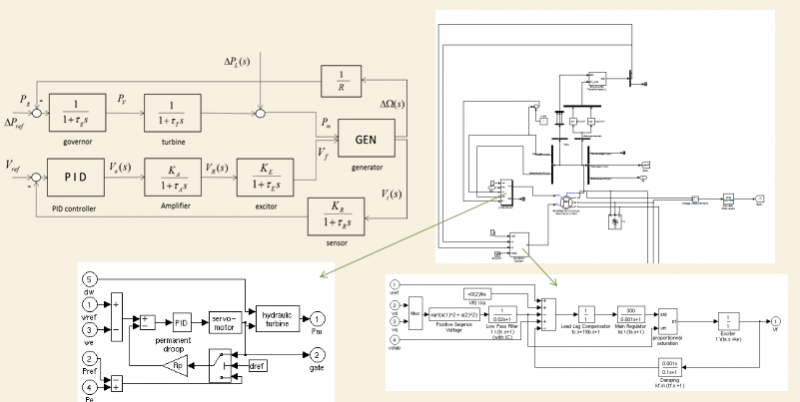
Figure 5. Flow chat and the implementation of genreation system

Besides the mentioned model, we also work on the communication layer and control layer. By combining them together, a cyber-physical network is obtained, and we could study the performance of the proposed approach for EDP by RT-lab, a real-time simulator.

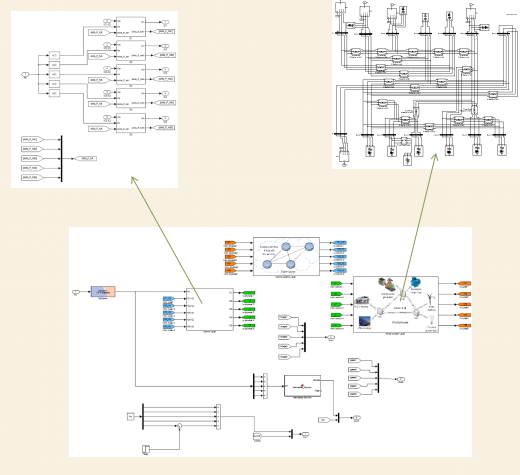
FIgure 6. Overall model in Matlab

3. Results

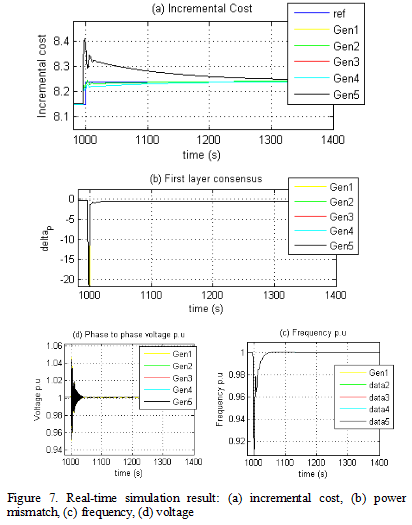
For solving EDP in power systems, the incremental cost of each generator is the crucial feature and it is also the second layer consensus in LICC algorithm. The first layer of consensus focus on estimating the global power mismatch (P). Phase to phase voltage and system frequency are also important factors to validate the algorithm. Figure 7(a) shows the convergence of incremental cost after load increase. Figure 7(b) shows the convergence of estimated global mismatch. Figure 7(c) and Figure 7(d) denote the response of system frequency and phase to phase voltage. Note that the main objective of this experiment is to demonstrate the feasibility of LICC on a detailed power system model. The control parameters on AGCs and AVRs are not optimal, which can be tuned to improve overall system performance on a case by case basis.

Figure 7(b), (c) and (d) proof the system stability and correction of the LICC implementation.

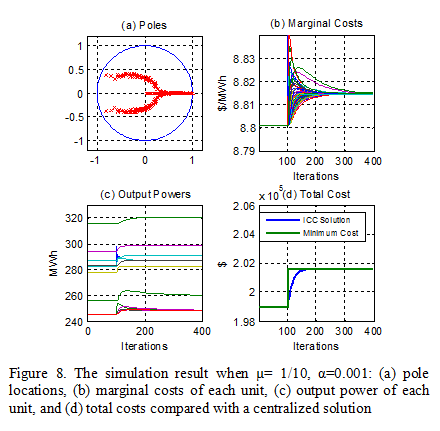
Scalability is one of the most important features of distributed algorithms. The performance of the LICC algorithm on a 100 nodes system has been demonstrated in Figure 8. To generate the local cost functions for 100 units, use the parameters shown in Table I and multiply each number by a random scalar u, where u~U (0.9, 1.1). The system starts from steady state with each node having 200MW loads. Loads have been increased at the 100th iteration on two buses. Since the LICC algorithm itself can be viewed as a discrete time linear system, location of poles of LICC can be used to determine the stability of the algorithm as Figure 8(a) demonstrated. Figure 8(b) shows that the incremental costs of 100 units are able to reach consensus on the new operation point in 500 iterations. Figure 8(c) shows the output power. We pick 10 units out of 100 to get a clear view of the characteristic of the algorithm. As Figure 8(c) shows, the generators that close to the bus that increased its demand first raise their output power; then the rest of the generators gradually increase the set points of their output power to share the load. The reason for this behavior is because when the network becomes large, the information takes more iterations to propagate. Figure 8 (d) shows the comparison of total cost.

4. Conclusion

The development of information and communications technology has enabled the use of distributed algorithms to manage networked control systems (or Cyber Physical Systems). In this paper we have extended the leader follower ICC algorithm to the LICC algorithm. The optimality and convergence have been derived. The steady state solution of the LICC algorithm is equal to the original constrained optimization problem.

The use of the LICC algorithm on the EDP has been demonstrated. It is a simple and effective approach for the power system to achieve distributed energy management without a control center or group leader. We have demonstrated the collective dynamic under different system configurations through simulations. The LICC algorithm itself can be analyzed by a discrete time linear system. Several parameters such as the weight of the updating matrix and µ can be used to control the group’s behavior. A power system model based on the IEEE 14 bus system with detailed generator dynamics has been developed in Matlab/Simulink as well as in RTLAB. The effectiveness of the LICC algorithm with generator dynamics on the detailed power system model has been tested. The scalability of the algorithm has been demonstrated through simulation on a large scale network.

Future directions includes further analysis of optimal weighting design under different communication topologies, generator controller tuning, and improve the resilience of the LICC algorithm under imperfect communication network.